
Identify apparent features of the pattern that were not explicit in the rule itself. Generate a number or shape pattern that follows a given rule. Determine whether a given whole number in the range 1-100 is prime or composite. Determine whether a given whole number in the range 1-100 is a multiple of a given one-digit number.

Recognize that a whole number is a multiple of each of its factors. Gain familiarity with factors and multiples.įind all factor pairs for a whole number in the range 1-100. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. Represent these problems using equations with a letter standing for the unknown quantity. Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison. Represent verbal statements of multiplicative comparisons as multiplication equations. Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Use the four operations with whole numbers to solve problems. Through building, drawing, and analyzing two-dimensional shapes, students deepen their understanding of properties of two-dimensional objects and the use of them to solve problems involving symmetry. Students describe, analyze, compare, and classify two-dimensional shapes. Students extend previous understandings about how fractions are built from unit fractions, composing fractions from unit fractions, decomposing fractions into unit fractions, and using the meaning of fractions and the meaning of multiplication to multiply a fraction by a whole number.ģ. They recognize that two different fractions can be equal (e.g., 15/9 = 5/3), and they develop methods for generating and recognizing equivalent fractions. Students develop understanding of fraction equivalence and operations with fractions. They select and accurately apply appropriate methods to estimate and mentally calculate quotients, and interpret remainders based upon the context.Ģ.

Students apply their understanding of models for division, place value, properties of operations, and the relationship of division to multiplication as they develop, discuss, and use efficient, accurate, and generalizable procedures to find quotients involving multi-digit dividends.
They develop fluency with efficient procedures for multiplying whole numbers understand and explain why the procedures work based on place value and properties of operations and use them to solve problems. Depending on the numbers and the context, they select and accurately apply appropriate methods to estimate or mentally calculate products. They apply their understanding of models for multiplication (equal-sized groups, arrays, area models), place value, and properties of operations, in particular the distributive property, as they develop, discuss, and use efficient, accurate, and generalizable methods to compute products of multi-digit whole numbers.

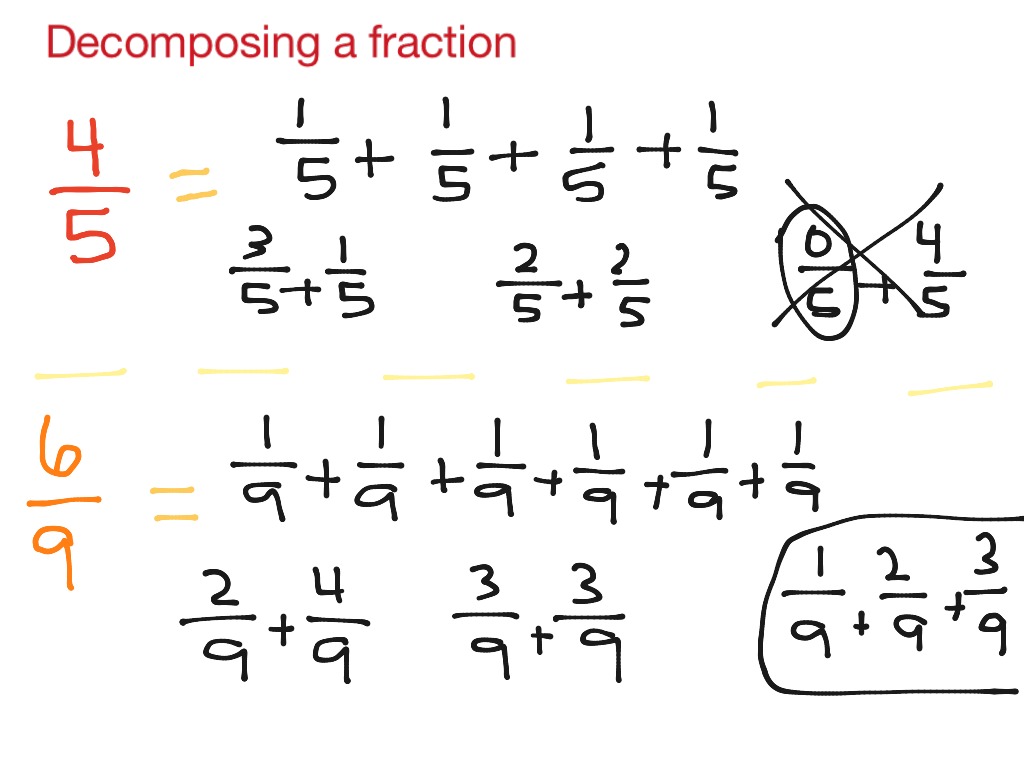
Students generalize their understanding of place value to 1,000,000, understanding the relative sizes of numbers in each place. The given context-about measuring fractional amounts using measuring cups of certain sizes-allows students to continue thinking in terms of equal groups, but also invites them to consider a fractional quantity as a sum of two or more fractions with the same denominator.In Grade 4, instructional time should focus on three critical areas: (1) developing understanding and fluency with multi-digit multiplication, and developing understanding of dividing to find quotients involving multi-digit dividends (2) developing an understanding of fraction equivalence, addition and subtraction of fractions with like denominators, and multiplication of fractions by whole numbers (3) understanding that geometric figures can be analyzed and classified based on their properties, such as having parallel sides, perpendicular sides, particular angle measures, and symmetry.ġ. This activity prompts students to think about non-unit fractions as being sums of other fractions. Previously, students considered non-unit fractions in terms of equal groups of unit fractions or as a product of a unit fraction and a whole number.


 0 kommentar(er)
0 kommentar(er)
